Speed Blindfolded Solving
Solving a Rubik's Cube blindfolded using a regular F2L (i.e. Fridrich) method.
March 12-25, 2006
My current record: 20:43 memorization, 18.04 execution

• Introduction • The Basic Idea • Examples • Cross • F2L: Tracing • Finishing up F2L • F2L: Tips and Tricks • OLL • Compound OLL • PLL •

This page will render incorrectly and slowly in Internet Explorer; use Firefox to view it.
You will also need a good computer running Java to view the demonstrative applets.

PLL

While most of speed BLD involves extensive tracing, trivial alg recognition, and more tracing through those recognized algs, PLL is the opposite. PLL recognition is the hardest part of the entire solve, though there is no more need to trace. Actually, it is even easy to feel confident in a wrong PLL. Half of my speed BLD DNF's were PLL mistakes (the others were F2L mistakes, and one was a horrible execution mistake) -I missed the world record with 16 minutes of memorization and 13 seconds of execution because of a three-corner cycle.
If you don't know all of PLL, I don't know what to tell you; depending on what you do know, there are different ways of resolving PLL (separate corners+edges, etc.). Try to be prepared for anything (because you really shouldn't be practicing or looking up algs during memorization).
You should probably figure recognition out yourself. Solve a cube up to OLL, and try to predict PLL. There is no single straightforward way to figure out the PLL (except to look at the cycles of the cube after OLL, +U, +U', and +U2 and recognize one of them as a PLL), so it's better if you figure out a way and accustom yourself to it. Nevertheless, for completeness, I'll try to explain some techniques I use to recognize PLL.

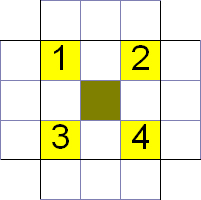
After OLL, you should have traced (or transposed, through compound OLL) all the LL pieces and know where they end up before PLL. You should remember the locations of both edges and corners in a standard order: I use UF-UL-UB-UR for edges and FL-ULB-UBR-URF for corners.
So, for example, UF (WR) ends up at UB, so I would remember the UB location as the first in the sequence. Then, UL lands in its home position, UL is second. For both corners and edges, I thus have an path of ordering in my mind (similar to regular BLD, but as orderings, not cycles). Note that such a path aways lands at the four different locations once.
As an example, here are the states of example #1 at PLL, represented by the images:

Example #1 after OLL actually looks like this. Of course, you do not actually see this, so you wouldn't immediately recognize the orange block. However, you can find it in the orderings: corner 2 and edge 3 are arranged as on the solved cube. The great thing about blocks is that they always help in PLL recognition: if you place the block, the other cycles will easily reveal PLL (except for the J -be vigilant all the time). But not all PLLs have blocks...
However, do try to keep in mind to search for block, however you recognize them. For this, ordering does work from every angle, but doesn't tell you how the other pieces are cycled. Thus, sooner or later, you will have to convert orderings to cycles.

#1: After OLL

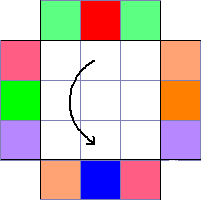Notice that UF (WR) is at UB. Thus, solving the piece involves moving the piece across the cube as indicated by the arrow in the picture on the right.

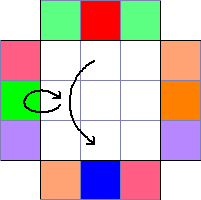The next piece, UL (WG) is in its home location, its cycle arrow returns to itself.

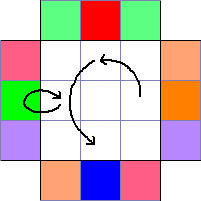The next piece, UB (WO) is at UR. Notice that this is building up a cycle, though not in order. You can do it that way, but just be aware of progress.

The last two edges give us the complete edge cycles for PLL.
Note that the edges form an Allan. Therefore, corners and edges must be independent. You could recognize and execute them separately, but only do this if you really need it (i.e speed memo).
Note also that if this did not form a valid edges-only PLL, then U or U' would make it so and thus make edges & corners independent.

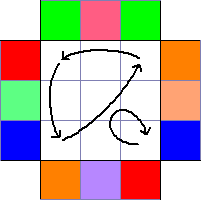The corner cycles are so; as I predicted, independent of EPLL.

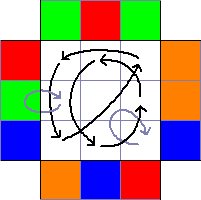These are all cycles together; they do not form a PLL in standard recognition position (where most often as many pieces are solved as possible). Note that a three-edge cycle and a three-corner cycle (as in this case) need not form a G.
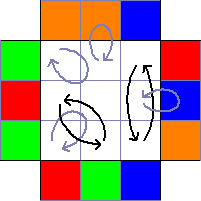Back to the idea of blocks, on the B face, a lot of cycling is going the same way, and you might now notice the orange block.

No matter how you recognize the block, you should rotate it into position with U' and recompute the cycles the same way (rearrange ordering, and create cycles piece by piece). Alternatively, you can try computing the cycles after adding a U, U', and U2 until you find a recognizable PLL. When you do this, first try to see which one seems to place the most pieces (since if it places a block, it will be in correct position).
Anyhow, you should soon arrive here, and find that it is an R PLL (my friend calls it the Phone). Now, all you have to do is memorize cube rotation and adjustment-of-the-U-face before the PLL, and the PLL.
If you want to actually finish by completely solving the cube in your head, go ahead and trace the pieces through PLL. It's not really necessary, though.

So for example #1, the entire PLL looks like this. Note that I do all adjustments-of-the-U-face turns before PLL

#1: PLL

This was the PLL for example #2.

#1: PLL

If, for some reason, no matter how carefully you try, you can not make sense of the PLL, you might have made a mistake. In this case, the number of even-length cycles for corners and edges should not be the same (if they are, keep looking). I once placed two F2L edges in each other's slots, and this happened to me.
I would suggest to first check any piece you are unsure of, or had to trace more than once for OLL.
If that doesn't work, don't stumble around for a patch, just go ahead and retrace every LL piece. Anything else less systematic will be more confusing and waste time. Trust me; I have a lot of experience in this.
If you are absolutely sure of your LL, the begin retracing F2L. First, make sure your cross is correct (if you never traced the cross pieces through cross moves, do it now). Then, trace each F2L pair to make sure you didn't make any mistakes there. Also make sure that you don't find any moves that you might have forgotten to apply to LL pieces during tracing (especially adjustments-of-the-U-face).
If you are terminally despondent, then try to predict something for PLL, and just do the solve as if you were certain. Guessing can't hurt, and is better than throwing it away by giving up. If you can film it, at least, just try the solve. If not, maybe just executing your solution moves slowly while looking at them might help. Don't get upset if you think you could have spotted the error easily; mistakes will occur sometimes. I remember when I was a three-cycle off on regular BLD for the Nationals; Chris Hardwick reassuringly told me, "It happens."